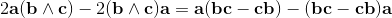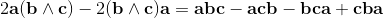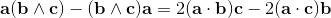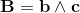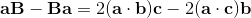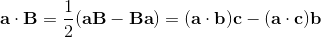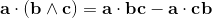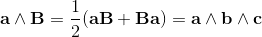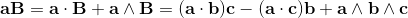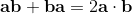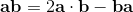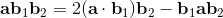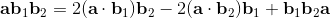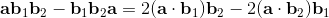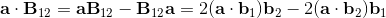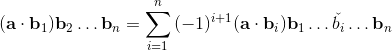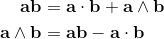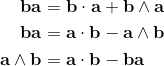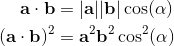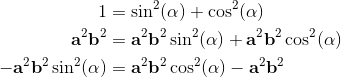Geometric Algebra and Lie-Algebra (Commutator Symbol)
Commutator Symbol
The commutator symbol is defined as [a,b] = ab-ba.
If we apply the commutator symbol on vectors a, b with the geometric product as operation,
we get the following expression for the outer product:
2a∧b = [a, b] = ab-ba;
2a∧b = [a, b] = -[b, a] = -(ba-ab) = -2b∧a;
2a∧a = [a,a] = aa - aa = 0;
λ[a, b] = [λa, b] = λ(ab - ba) = [a, λb];
[a+b,c] = [a,c] + [b,c] = (a+b)c - c(a+b) =
ac + bc - ca - cb = (ac - ca) + (bc - cb);
[a, [b, c]] = a(bc - cb) - (bc - cb)a = abc - acb - bca + cba;
[[a, b], c] = (ab - ba)c - c(ab - ba) = abc - bac - cab + cba;
Jacobi Identity:
[a, [b, c]] + [b, [c, a]] + [c, [a, b]] = 0;
[a, bc - cb] + [b, ca - ac] + [c, ab - ba] = 0;
(abc - acb) - (bca - cba) + (bca - bac) - (cab - acb) + (cab - cba) - (abc - bac) = 0;
abc - abc + acb - acb + bca - bca + cba - cba + bac - bac + cab - cab = 0;
Anticommutator Symbol
2a⋅b = {a, b} = ab + ba;
The Geometric Product with Commutator and Anticommutator Symbol
2ab = 2a⋅b + 2a∧b = {a, b} + [a, b] = ab + ba + ab - ba;
Motivation for a Lie-Algebra
With a matrix A we can define a element a = (I+εA) and
a second element b = (I+εB) from a matrix B, both close to the identity element I for small ε.
The product will be:
ab = (I+εA)(I+εB) = I + ε(A+B) +ε2AB;
If we ingnore the AB term because ε2 is very small we get:
ab = I + ε(A+B);
With a-1 = (I+εA)-1 = I - εA + ε2A2 - ε3A3... ;
For non commutating elements a,b the expression aba-1b-1 is not equal I. We can express this term as follows:
aba-1b-1 = (I+εA)(I+εB)(I - εA + ε2A2)(I - εB + ε2B2);
Suppressing terms with εn and n>2 will give:
aba-1b-1 = I + ε2(AB - BA).
Definiton of a Lie Group can be found on the Abstract Algebra page:
Lie Group

 English
English
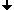
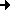

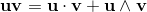
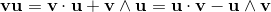
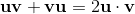
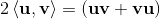
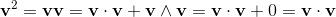
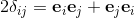
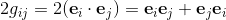
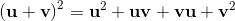 (1)
(1)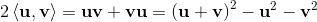 (2)
(2)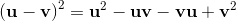 (3)
(3)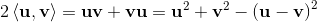 (4)
(4)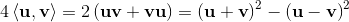 (5)
(5)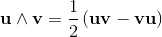
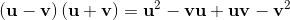 (6)
(6)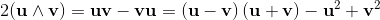 (7)
(7)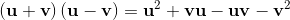 (8)
(8)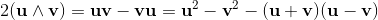 (9)
(9)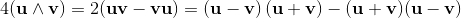 (10)
(10)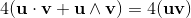
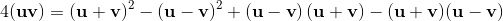
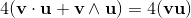
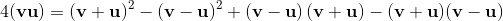

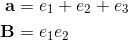
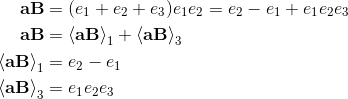
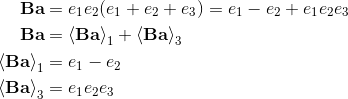
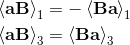
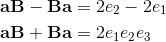
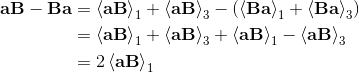
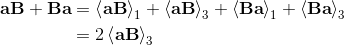
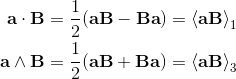
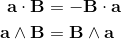
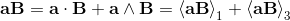
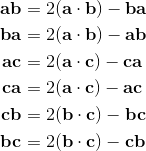
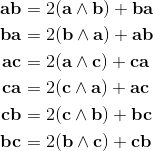
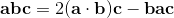
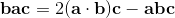
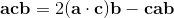
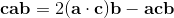
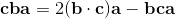
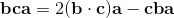
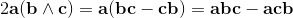
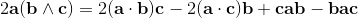 (1)
(1)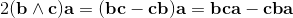
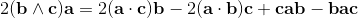 (2)
(2)