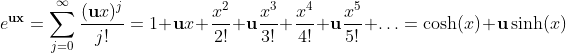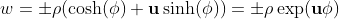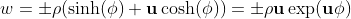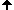Attention

This page has been tested and developed with the Mozilla browser. This page requires JavaScript in your browser. Without JavaScript or JavaScript beeing disabled, the display of this side is incomplete.

Prolog

Die rote oder die blaue Pille?

References

This page is based on the concepts developed on my geometric algebra page and on my linear algebra page.

Linear Algebra

Geometric Algebra

Clifford Algebra

Hypercomplex Numbers

Matrix Representation of the Canonic Base Elements of the Geometric Algebra 𝔾²

A vector v ∈ ℝ² can be written in the following form, using the unit vectors e₁, e₂:

v = v₁e₁ + v₂e₁

From the base vectors e₁, e₂ the canonic elements of the geometric algebra 𝔾² can be derived.

Scalar: I = I₍₀₎, Vectors: e₁, e₂, Pseudoscalar(element with highest grade): I₍₂₎=e₁e₂=e₁∧e₂.

Algebraic Relations of the Canonic Base Elements in the Geometric Algebra 𝔾²

(e₁e₂)² = (e₁∧e₂)² = -I;

e₁² = I;

e₂² = I;

(e₁∧e₂)e₂ =  e₁;

e₂(e₁∧e₂) = -e₁;

e₁(e₁∧e₂) =  e₂;

(e₁∧e₂)e₁ = -e₂;

-e₁e₂ = -(e₁∧e₂) = e₂∧e₁ = e₂e₁;

(e₂e₁)² = (-e₁e₂)² = -I

Matrix Form of the Canonic Elements of 𝔾²

The canonic elements of the geometric algebra 𝔾² can be written in matrix form. These matrices have the same algebraic properties as the canonic elements of 𝔾².

These four matrices form a group.

The three matrices are the same as the three matrices for reflection and 90° rotation. Visit the rotation matrix page for details.

Rotation Matrices

Algebraic Relations between 𝔾² Base Elements and the Matrix Representation of these Elements

(e₁e₂)² = (e₁∧e₂)² = -I;

e₁² = I;

e₂² = I;

(e₁∧e₂)e₂ =  e₁;

e₂(e₁∧e₂) = -e₁;

e₁(e₁∧e₂) =  e₂;

(e₁∧e₂)e₁ = -e₂;

-e₁e₂ = -(e₁∧e₂) = e₂∧e₁ = e₂e₁;

Complex Numbers as Matrices

A complex unit called i is the solution of the expression:

x² + 1 = 0; ⇔ x² = -1; ⇔ x = ±√-1 = ±i;

and has the property:

(±i)² = -1

A Matrix as Complex Unit

A Complex Number can be Represented as Matrix

The Complex Conjugate in Matrix Form

The Product of two Complex Numbers as Matrix Product

Using the matrix representation of two complex numbers z₁, z₂ will give the following product:

Polar Form of a Complex Number

The exponential presentation of a complex number z looks as follows:

z = e^a+iθ = e^ae^iθ = e^a(cos(θ) + isin(θ)) = e^acos(θ) + ie^asin(θ)

Expressing this equation in matrix form will give:

Using e^a = r;

Complex Numbers and Geometric Algebra

Hyperbolic Numbers in Matrix Form

Hyperbolic unit called u is the solution of the expression:

x² - 1 = 0

and has the following properties:

u² = 1 and u ≠ ±1

A hyperbolic number w can be expressed as matrix.

It has the conjugate w that has the following matrix form:

Which is equivalent to:

ww = (x+uy)(x-uy) = x²-y².

Calculation of the Inverse of w

Hyperbolic Polar Form

Exponential function with hyperbolic unit

Hypebolic numbers can easiely expressed in hyperbolic polar form.

For quadrants I and III we have:

For quadrants II and IV we have:

Hyperbolic Units in Matrix Form

uu = uu = u(-u) = (-u)u = -I

Polar Form of a Hyperbolic Number

w = e^a+uθ = e^ae^uθ = e^a(cosh(θ) + usinh(θ)) = e^acosh(θ) + ue^asinh(θ);

Expressing this equation in matrix form will give:

Using e^a = r;

Chromogeometry - Complex Numbers in Matrix Form

Chromogeometry is a generalisation of the matrix representation of complex numbers. Also known as split quaternions.

When you take the building matrices for the matrix representation of the geometric algebra 𝔾²:

it is possible to construct three different subalgebras named blue, red, green:

These matrices build commutative subalgebras of the 2x2 matrices.

They have the properties:

i2 = -I u2 = I h2 = I

ui = h, iu = -h ih = u, hi = -u uh = i, hu = -i

The three Matrices blue red and green can be interpretated as two reflections in the blue and red case and as a rotation in the green case.

Reflection and Rotation

Dihedron Algebra

This is a quadratic invers algebra over a field 𝔽 an algebra with a multicative quadratic form that controls the inverses.

D ∈ 𝔻

Relation between a Determinant and a Quadratic Form

Only in the case of the 2x2 matrices there is a special relation between the trace of a matrix A and a quadratic form Q(A).

det(A) = ad-bc = Q(A);   (In 2-dimensions the determinant is equal to a quadratic form)

A₁, A₂ ∈ 𝔻;

det(A₁A₂) = det(A₁)det(A₂);

det(A) = Q(A) =>

Q(A₁A₂) = Q(A₁)Q(A₂);

Polarisation Identity

w, v ∈ 𝔻;

Q(w+v) = (w+v)·(w+v) = w·w + v·v + 2w·v;

2w·v = Q(w+v) - Q(w) - Q(v);

In the two dimensional case the quadratic form Q(v) = det(v) (only in 2 dimensions):

2w·v = det(w+v) - det(w) - det(v)

Scalar Product and the Trace

Take the sum of two dihedrons

Calculate the quadratic forms.

Q(r₁+r₂) = det(r₁+r₂) = (a₁+a₂)(d₁+d₂) - (b₁+b₂)(c₁+c₂);

Q(r₁) = det(r₁) = a₁d₁-b₁c₁

Q(r₂) = det(r₂) = a₂d₂-b₂c₂

Calculating the scalar product by the use of the polarisation identity:

2r₁·r₂ = det(r₁+r₂) - det(r₁) - det(r₂) = a₁d₂ + a₂d₁ -b₁c₂ - b₂c₁;

Calculating the product of a Dihedron and the Adjoint of a Dihedron:

Calculating the trace of the product and compare it with the result of the scalar product gives:

2r1·r2 = trace((r1)(r2)adj) = a1d2 + a2d1 - b1c2 - b2c1;

The result is also known as the scalar dot product.

Adjoint of a Dihedron

The adjoint r^adj of a 2x2 matrix r is defined as follows:

The product of a dihedron r with its adjoint r^adj gives:

(r₁r₂)^adj =(r₂)^adj(r₁^)adj

Dihedron Group

Set of the Dihedron Group: 𝔾: {±I, ±i, ±u, ±h}

Product of the Dihedron Group

Idempotent Base

The standard base for hyperbolic numbers w is {1,u}. An alternative to this base is the idempotent base of the hyperbolic numbers w is the pair {u₊, u_-}.

Now we have two ways to represent a hyperbolic number:

The idempotent base elements are defined in the relation to the standard base elements as follows:

The new indempotent base elements {u₊,u_-} have the idempotent and the annihilation properties.

Idempotent Property

The elements u₊ and u_- are idempotent because (u₊)² = u₊ and (u_-)² = u_-.

Annihilating Property

The elements u₊ and u_- are mutually annihilating because u₊u_- = 0.

Spectral Decomposition of Hyperbolic Numbers

The decomposition of w = w₊u₊ + w_-u₊ is the spectral decomposition of w = x + uy. Where the spectral weight elements w₊ and w_- are defined as follows:

The the weight elements x and y of standard base {1,u} of the hyperbolic numbers can be calculated from the weight elements w₊, w_- of the idempotent base {u₊,u_-}.

Spectral Decomposition

With the following spectral components:

Details

Product

The product of the spectral weight element w₊ and w_- is:

Applications

The product of two hyperbolic numbers is:

vw = (v₊u₊ + v_-u_-)(w₊u₊ + w_-u_-) = (v₊w₊)u₊ + (v_-w_-)u_-

The binomial theorem gives a very simple form with the idempotent basis. Hence the powers of hyperbolic numbers can be easy computed.

(w₊u₊ + w_-u₁)^k = (w₊)^k(u₊)^k + (w_-)^k(u_-)^k = (w₊)^ku₊ + (w_-)^ku_-

Pauli Matrices

The Pauli matrices contain the complex element i with the property i² = -1.

Properties of the Pauli Matrices

σ₀ = I;

(σ₀)² = (σ₁)² = (σ₂)² = (σ₃)² = I;

(σ₁₂)² = (σ₂₃)² = (σ₃₁)² = -I;

σ₁σ₂σ₃ = iI = I₍₂₎;

(σ₁₂₃)² = (I₍₂₎)² = -I

σ₁σ₂ = iσ₃;

σ₂σ₃ = iσ₁;

σ₃σ₁ = iσ₂;

Matrix Calculations

Preforming the matrix calculations:

Pauli Matrices and Quaternions

The following relationship between the Pauli matrices and the quaternions exists:

i = iσ₁; j = -iσ₂; k = iσ₃;

With these relations it is possible to define the quaternions as two by two matrices with complex elements:

Quaternions

Pauli Matrices and the Geometric Algebra 𝔾³

The following relation between the Pauli matrices and the Geometric Algebra 𝔾³ exists:

e_ie_j = δ_ij + I₍₃₎ε_ijke_k ⇔ σ_iσ_j = δ_ij + iε_ijkσ_k

Pauli matrices as 4x4 matrices can be found here:

4x4 Pauli Matrices

Matrix Representation of the Canonic Base Elements of the Geometric Algebra 𝔾³

More information on the geometric algebra 𝔾³ can be found on my geometric algebra page. The geometric algebra 𝔾³ has a strong relation to quaternions.

A vector v ∈ ℝ³ can be written in the following form, using the unit vectors e₁, e₂, e₃ :

v = v₁e₁ + v₂e₁ + v₃e₃

Using 4×4 matrices to define I, e₁, e₂, e₃ and the unit psuedoscalar e₁₂₃ = I₍₃₎.

Relation to Quaternions

The bivectors -e₁₂, -e₂₃, -e₃₁ are equivalent to the quaternions. These bivectors have the same algebraic properties as the quaternions.

Using the unit pseudo scalar I₍₃₎ as imaginary unit we get the following relations to the quaternions:

i = -I₍₃₎e₁;   j = -I₍₃₎e₂;   k = -I₍₃₎e₃;

Geometric Numbers

Geometric numbers comprise the real numbers and two new elements a,b with special properties. The new geometric numbers a,b also called g-numbers have the following properties:

(i)  a²=0=b² The new g-numbers are called nilpotent or null vectors.

(ii) 2a‧b =ab+ba=1

The g-Numbers Expressed as Matrices

The canonic elements a and b expressed as matrices:

Squaring of the canonic matrices will result in the zero matrix:

a² = 0;

b² = 0;

Building the product a and b and the product b and a.

ab

ba

The products ab and ba expressed as matrices:

ab + ba = 1

ab - ba = -h

aba=(ab)a=(1-ba)a=a-ba²=a

bab=(ba)b=(1-ab)b=b-ab²=b

(ab)²=(1-ba)ab=ab+ba²b=ab

(ba)²=(1-ab)ba=ba+ab²a=ba

(ab)(ba) = 0 = (ba)(ab)

From the above properties the multiplication table for basic g-numbers a, b, ab, ba can be dereived.

	a	b	ab	ba
a	0	ab	0	a
b	ba	0	b	0
ab	a	0	ab	0
ba	0	b	0	ba

The basic g-numbers can be written in a matrix form:

We have the following matrices for a, b, ab and ba:

The general form of a g-matrix is as follows:

A geometric number g can know be expressed as follows.

Conjugation and Inversion

Each g-number can be seen as the sum of two parts g = g_o + g_e the odd part g_o and the even part g_e.

The odd part of a g-number looks as follows:

The even part of a g-number looks as follows:

The reverse of a g-number

With (ab)^† = ba the reverse operation for the odd and the even part are defined as follows:

g_o^† = g_o

g_e^† = g₁₁ab + g₂₂ba

The reverse of a g-number has the following property:

g^† = (g_o + g_e)^† = g_o^† + g_e^† = g_o + g_e^†

Hence we have for g^†

The inverse of a g-number

The invers of a g-numger is named g^- and has the following properties:

g^-_o = -g₁₂b - g₂₁a; for the odd part.

g^-_e = g_e; for the even part.

The sum of the even and the odd part will give g^-

g^- = (g_o + g_e)^- = g^-_o + g^-_e = -g_o + g_e

Hence we have for g^-

Mixed conjugation

The combination of the operations of reversion and inversion of a g-number will give the mixed conjugation g^*.

g^* = (g^†)^- = (g_o + g_e^†)^- = -g_o + g_e^†

Geometrie of a and b

Construction of the geometric algebra 𝔾² with the nilpotent 2x2 matrices a and b.

The relations between these matrices can be found by the matrix representation of the geometric algebra 𝔾²

Odd Number Plane

Even Number Plane

Determinants and the Outer Product

Outer Product of two Vectors and the Determinant

Bulding the outer product of two vectors u and v gives:

u ∧ v = (u₁e₁ + u₂e₂) ∧ (v₁e₁ + v₂e₂) = (u₁v₂ - u₂v₁)(e₁∧e₂);

The first term on the right side (u₁v₂ - u₂v₁) is the value of the determinant:

Outer Product of three Vectors and the Determinant

Bulding the outer product of three vectors u, v and w gives:

u ∧ v ∧ w = (u₁e₁ + u₂e₂ + u₃e₃) ∧ (v₁e₁ + v₂e₂ + v₃e₃) ∧ (w₁e₁ + w₂e₂ + w₃e₃) = (u₁v₂w₃ + v₁w₂u₃ + w₁u₂v₃ - w₁v₂u₃ - v₁u₂w₃ - u₁w₂v₃) (e₁∧e₂∧e₃);

The first term on the right side (u₁v₂w₃ + v₁w₂u₃ + w₁u₂v₃ - w₁v₂u₃ - v₁u₂w₃ - u₁w₂v₃) is the value of the determinant.

Outer Product of n-Vectors and the Determinant

The outer product of n-vectors is the derminant of the matrix with the n vectors as column vectors multiplied with the unit pseudoscalar I_(n)

Definition of the Determinant in Linear Algebra

The Determinant in Geometric Algebra

The next page is about hypercomplex numbers.

Hypercomplex Numbers